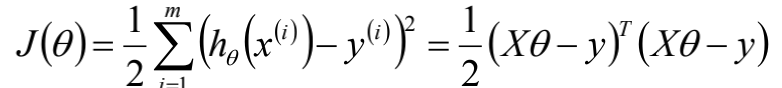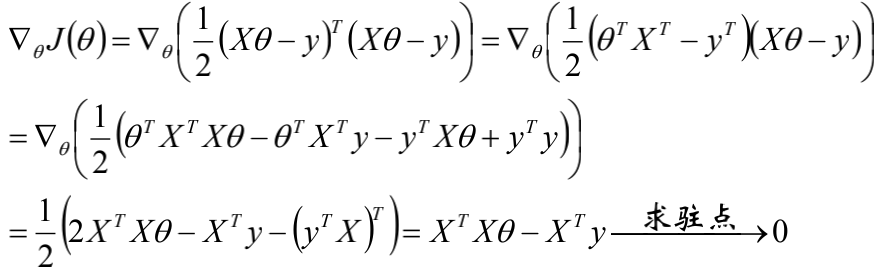线性回归
对于单个变量:
y=ax+b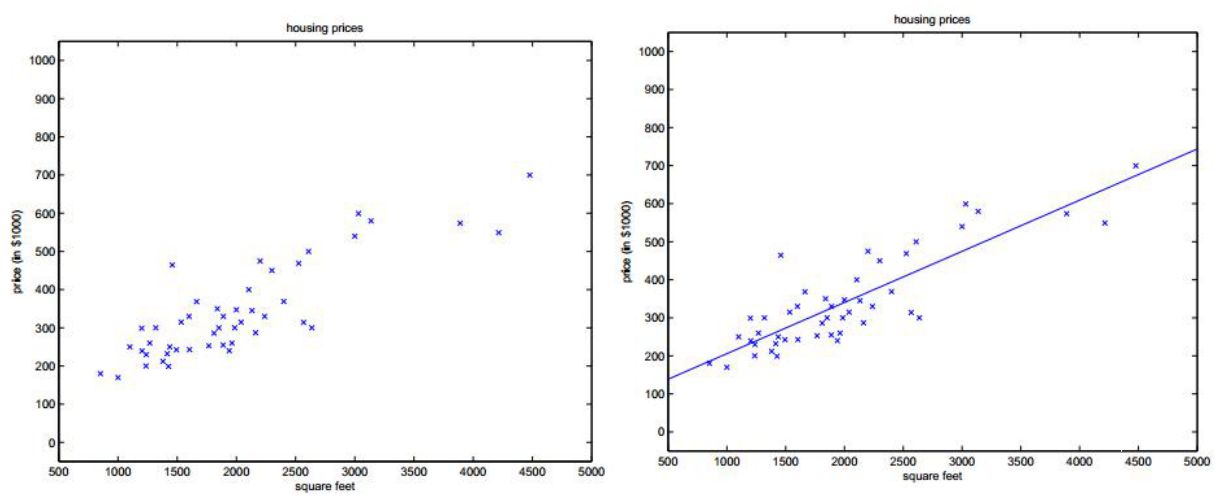
对于多个变量: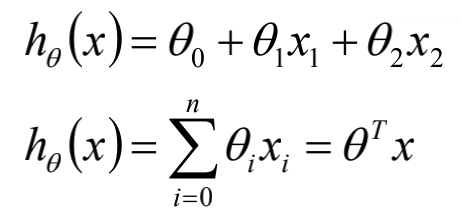
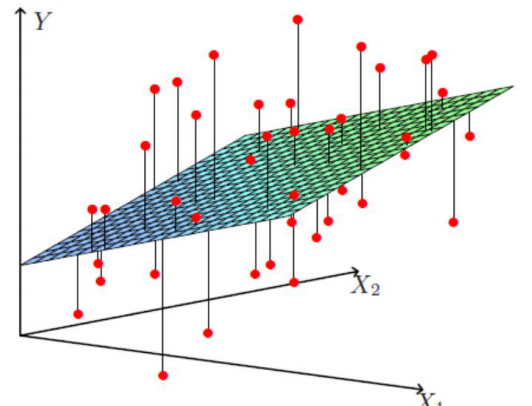
使用极大似然估计解释最小二乘法
误差是独立同分布的,服从均值为0,方差为某定值的高斯分布。
原因:中心极限定理
中心极限定理的意义
在实际问题中,很多随机现象可以看做众多因素独立影响的综合反应,往往近似服从正态分布。
- 应用前提是多个随机变量的和,有些问题是乘性误差,则需要鉴别或者取对数后使用。
似然函数
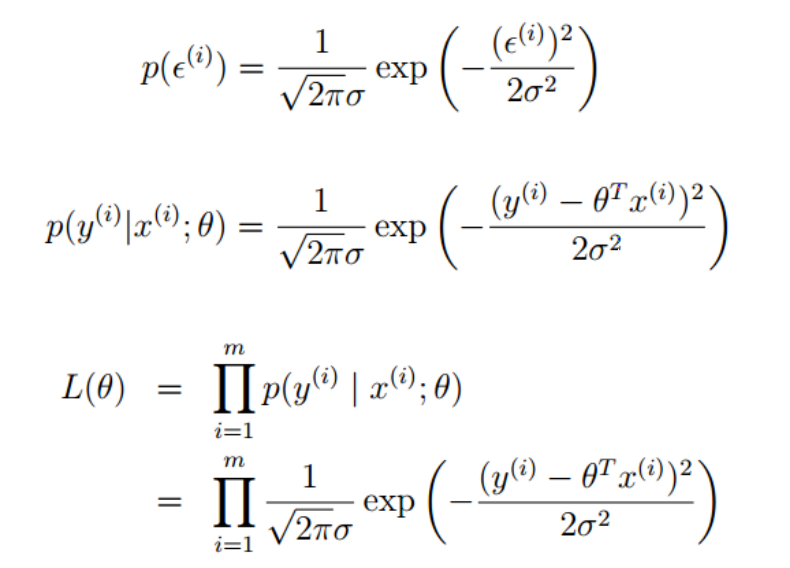
高斯的对数似然与最小二乘
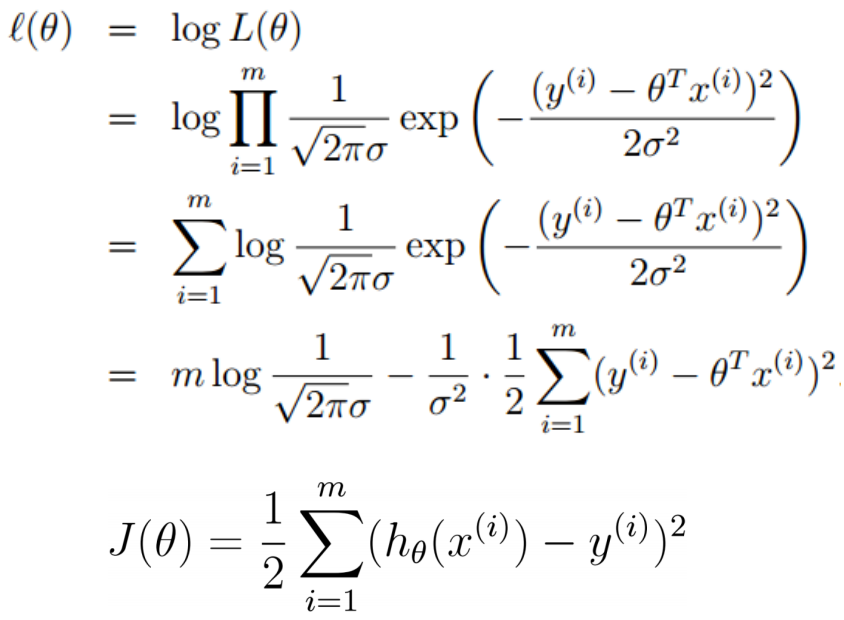
###的解析式求解过程
将M个N维样本组成矩阵X:
- x的每一行对应一个样本,共M个样本(measurements)
- X的每一列对应样本的一个维度,共N维(regressors)
- 还有额外的一维常数项,全为1
目标函数
梯度
最小二乘意义下的系数最优解
参数的解析式: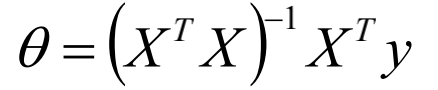
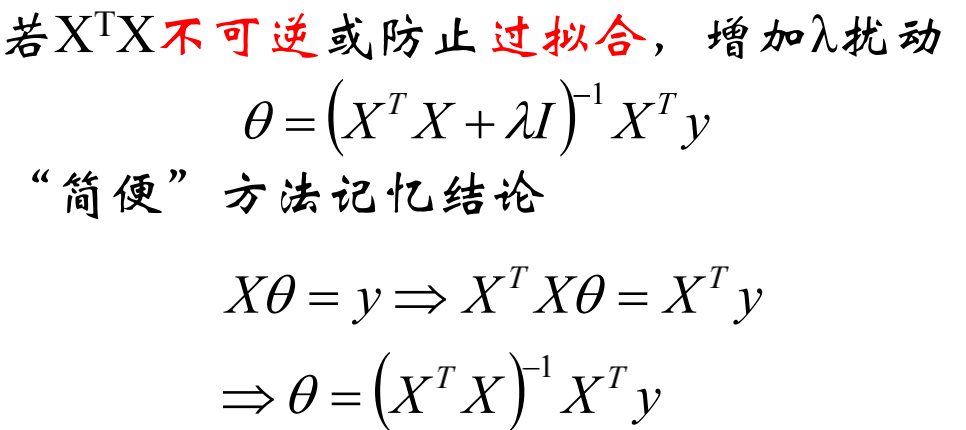
加入扰动后:
半正定:对于任意非零向量u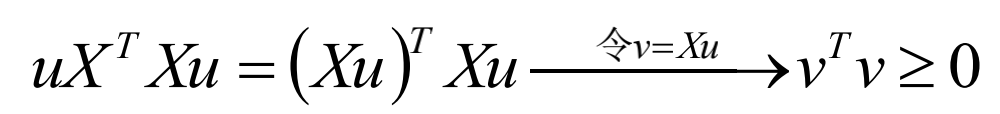
所以,对于任意实数\lambda>0,正定,从而可逆,保证回归公式有意义。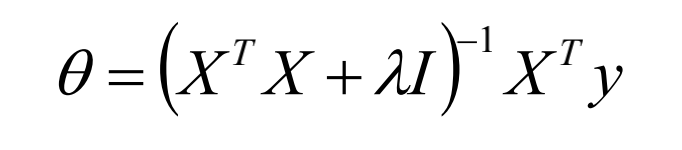
线性回归的复杂度惩罚因子
线性回归的目标函数为:
将目标函数增加平方和损失;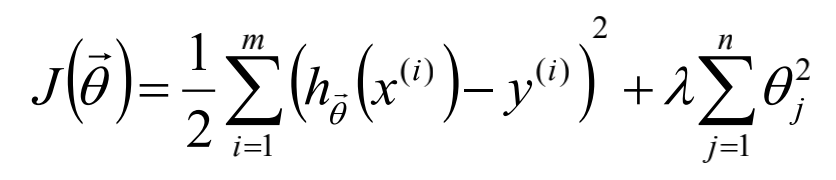
本质即为假定参数服从高斯分布。