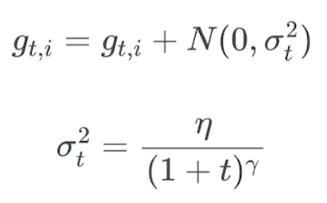cv学习笔记梯度下降优化算法

梯度下降法

• 梯度下降法是训练神经网络最常用的优化算法
• 梯度下降法（Gradient descent） 是一个一阶最优化算法，通常也称为最速下降法。要使用梯度下降法找到一个函数的局部最小值，必须想函数上当前点对应的梯度(或者是近似梯度)的反方向的规定部长距离点进行迭代搜索。
• 梯度下降法基于以下的观察：如果实值函数$f(x)$在a点处可微并且有定义，那么函数$f(x)$在点a沿着梯度相反的方向$-\nabla f(a)$下降最快

$$\theta = \theta -\eta \cdot \nabla _{\theta}J(\theta)$$

偏导数

对于一个多元函数，比如$f(x,y)=x^2y$,计算偏导数：

将不求的部分当做常数，其他部分求导即可。

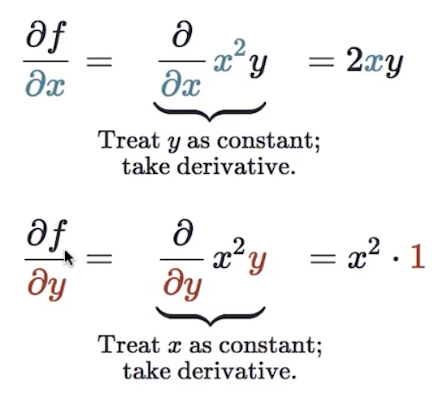
梯度

The gradient of a scalar-valued multivariable function$f(x,y,...)$,denoted$\nabla f$,packages all its partial derivative information into a vector:

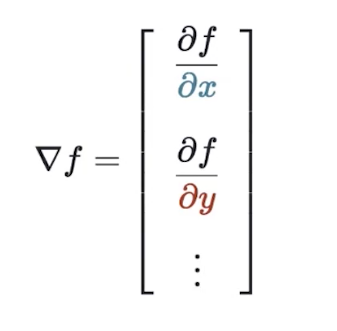
这就意味着$\nabla f$是一个向量。

梯度下降算法

在每一个点计算梯度，向梯度相反的方向移动指定的步长，到达下一个点后重复上述操作。

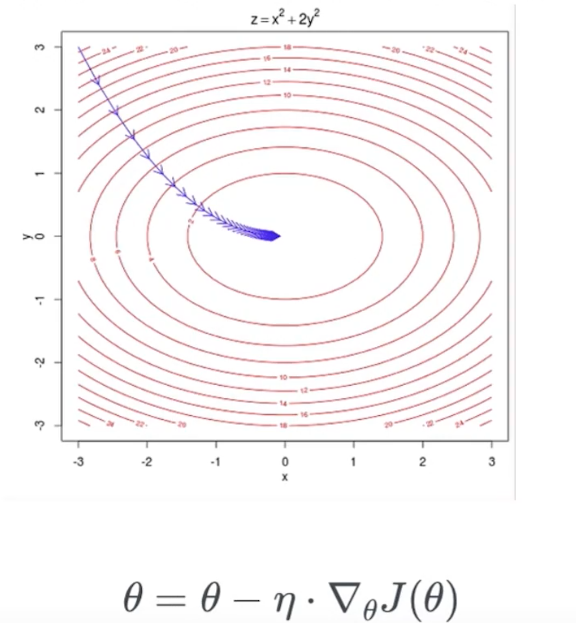
批处理梯度下降法

有两层循环，伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12

for i in range (nb_epochs):
#最外层循环用来不断更新参数。
  sum_grad = 0   #定义变量梯度求和，注意此处应为向量，而非实数值
  for x, y in data: #x是训练数据的输入，y是label
    grad = gradient(loss_function, x, y, params)
    #x,y,params是损失函数的参数
    # params 是参数，可以是卷积核的权值或者神经网络的权值
    sum_grad += grad
  avg_grad = sum_grad/len(data)
  #获得平均梯度
  params = params - learning_rate * avg_grad
  #learning_rate是步长，或称为学习率

特点

• 在凸优化(Convex Optimization)的情况下，一定会找到最优解
• 在非凸优化的情况下，一定能找到局部最优解
• 单次调整计算量大
• 不适合在线(Online)情况

随机梯度下降法

有两层循环，伪代码如下:

1
2
3
4
5
6
7
8

for i in range(nb_epochs):
  np.random.shuffle(data)
  for x, y in data:  #x是训练数据的输入，y是label
    grad = gradient(loss_function, x, y, params)
    #x,y,params是损失函数的参数
    # params 是参数，可以是卷积核的权值或者神经网络的权值
    params = params - learning_rate * avg_grad
    #learning_rate是步长，或称为学习率

与批处理相比，梯度更新在第二个循环内部，所以参数更新次数增多了。

每一次循环前有一次shuffle，遍历的顺序是随机的。

特点

• 适合Online的情况
• 通常比批处理下降法快（在批处理的情况下，有可能许多数据点产生的梯度是相似的，属于冗余运算，并没有实际帮助）
• 通常目标函数震荡严重，在神经网络优化情况下（没有全局最优解），这种震荡反而有可能让它避免被套牢在一个局部最小值，而找到更好的局部最优解
• 通过调整学习率，能够找到和批处理相似的局部或者全局最优解

迷你批处理梯度下降法

有三层循环，伪代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

for i in range(nb_epochs):
  np.random.shuffle(data)
  for mini_batch in get_mini_batch(data, batch_size = 50): 
   #batch_size 表示mini_batch的数量
   sum_grad = 0   
  #定义变量梯度求和，注意此处应为向量，而非实数值
    for x, y in mini_batch: 
      #x是训练数据的输入，y是label
        grad = gradient(loss_function, x, y, params)
        #x,y,params是损失函数的参数
        # params 是参数，可以是卷积核的权值或者神经网络的权值
        sum_grad += grad
    avg_grad = sum_grad/len(data)
    #获得平均梯度
    params = params - learning_rate * avg_grad
        #learning_rate是步长，或称为学习率

特点

• 结合了批处理和随机梯度下降法的优点
• 减弱了目标函数震荡，更加稳定
• 易于硬件加速实现，常用的机器学习库都利用了这个特性提供了高性能的计算速度（mini批可能能够放入GPU显存或者内存）
• 一般的迷你批大小位50至256，取决于不同的应用

传统梯度下降法面临的挑战

• 传统迷你批处理不能保证能够收敛
• 当学习率太小，收敛会很慢，学习率太高，容易震荡，甚至无法收敛
• 可以按照某个公式随着训练逐渐减小学习率，但是不同数据集需要不同的学习率变化曲线，不容易估计
• 所有的参数使用同样的学习率并不合适
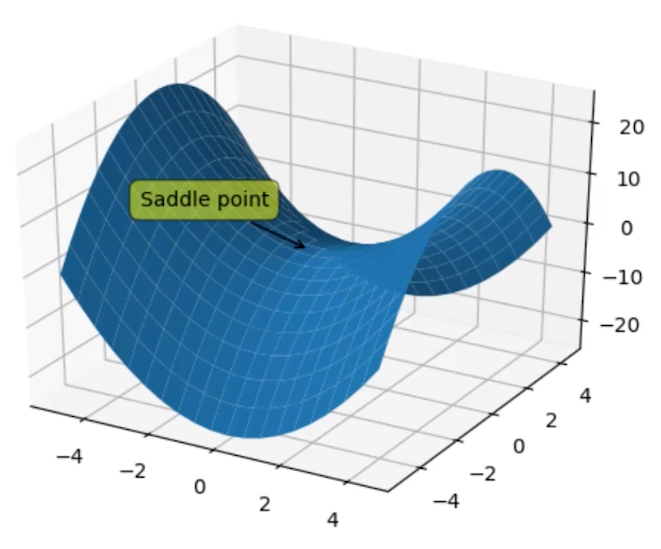
• 容易被套牢在马鞍点(Saddle point)

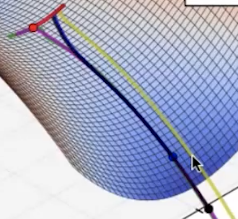
马鞍点

在马鞍点处，梯度为0，但是不是最优解。不同算法有些能够逃离，有些不能逃离。

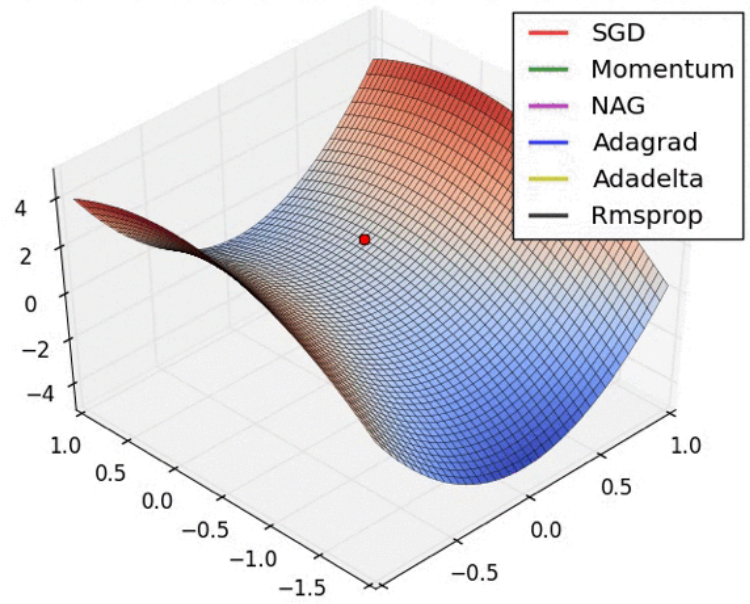
在这种马鞍点中，Adadelta较容易逃离，NAG、Rmsprop、Adagrad、Momentum都可以逃离，随机梯度下降法（SGD）无法逃离。

常见的梯度下降法

Momentu（动量法）

• 不同的dimension的变化率不一样
• 动量在梯度的某一纬度上的投影只想同一方向上的增强，在纬度上的指向不断变化的方向抵消
  *$v_t = \gamma v_{t-1}+\eta \nabla _{\theta}J(\theta)$

$\theta = \theta - v_t$

$\gamma :=0.9$

以中药碾子为例：

假设中心凹槽为曲面，那么最优值应该在中心位置：

如果不引入Momentum，那么训练过程中，移动方向会不断向两侧跳跃：

如果引入Momentum：

为什么能达到这样的效果

将曲面画作山谷形状，理想情况下是蓝色曲线的路径：

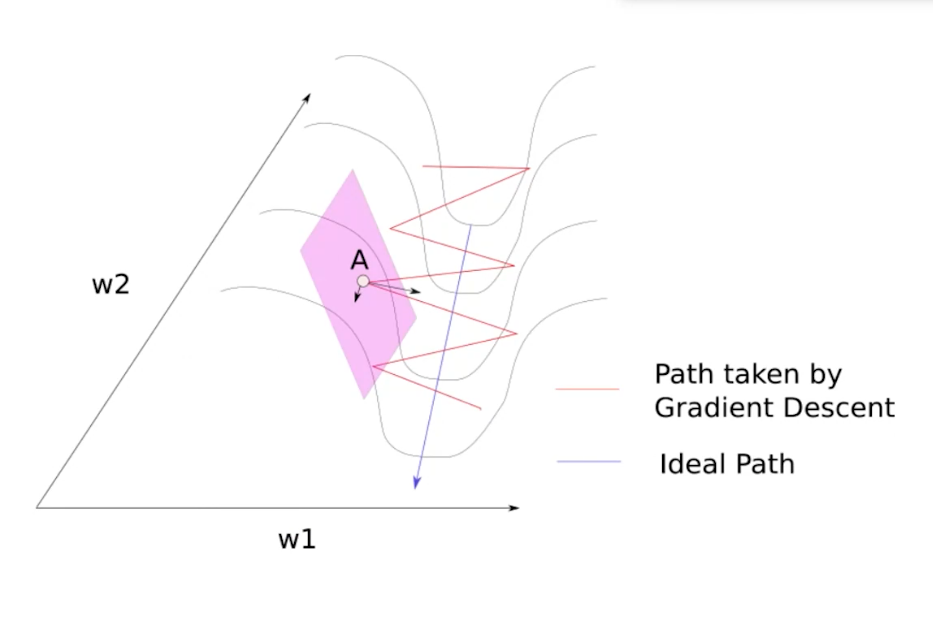
但是在传统算法，那么运动的曲线为红色曲线。如果我们将每一个点按照参数方向进行分解：

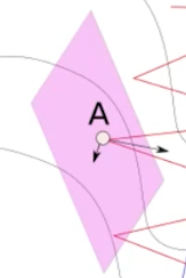
在每一点都进行分解：

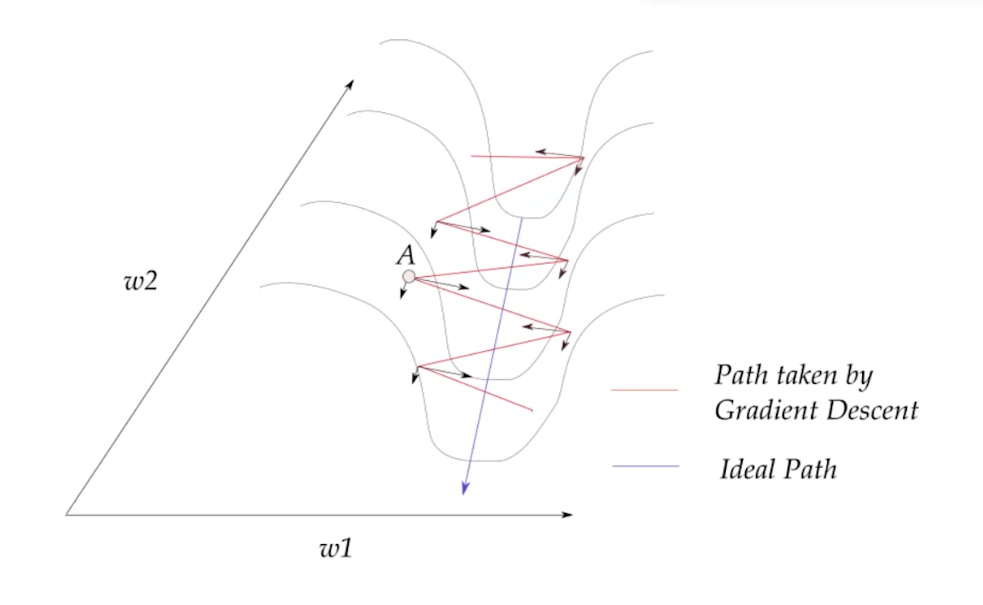
可以看到，任何一点都有一个分方向与最优方向同向，另一个分方向会与下一个分方向部分抵消。这样最优方向的分向会增加，其他方向会逐渐抵消。

Nesterov accelerated gradient

• 动量+预测前方的梯度
• 在多个RNN任务中表现突出
  *$v_t = \gamma v_{t-1}+\eta \nabla _{\theta}J(\theta -\gamma v_{t-1})$

$\theta = \theta - v_t$

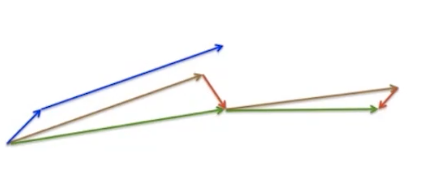
小结

上面两种优化算法都是对梯度本身的优化，整体优化，下面的几种方法将采用对参数“各个击破的方式”来实现优化。

Adagrad

• 对重要性高的参数，采用小的步长
• 对相对不重要的参数，采用大的步长
• 对稀疏数据集非常有效（文本数据）。Google在训练从Youtube识别自动识别猫采用的就是这种方法，Pennington et al训练词嵌入的GloVe也采用的这种方法

实现方法

$g_{t,i} = \nabla J(\theta _t , I)$

$\theta _{t+1},I = \theta ,I- \frac{\eta}{\sqrt{G_{t,ii}+\epsilon}}\cdot g_{t,i}$

关键在于分母，$G_t$是一个$d\times d$对角矩阵，d表示参数的个数。$G_{t,ii}$表示第$i$个参数位置的值

$G_{t,ii}=({\theta _i})_t ^2+({\theta _i})_{t-1}^2+...$

为了防止G为0，加入另外一个很小的值$\epsilon$

优势

• 无需手动调整步长
• 设置初始值为0.01即可

劣势

• 随着训练，步长总是越来越小

Adadelta

• 只累积过去一段时间的梯度平方值
• 完全无需设置步长
• 为了便于实现，采用类使用动量的策略：

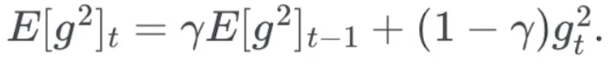
实现方法

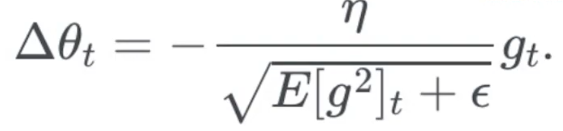
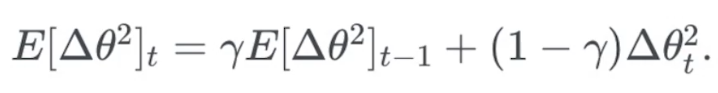
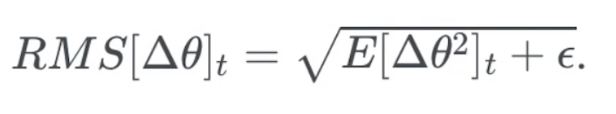
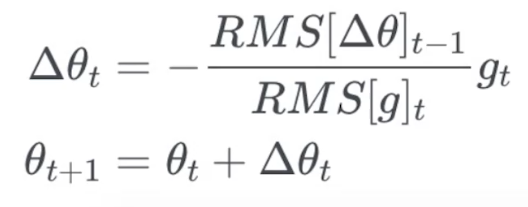
RMSprop

与上面两种方法几乎一致，把过去结果乘0.9，当前结果乘0.1

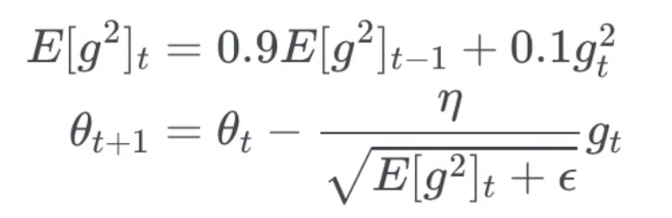
公式不同，思路相似

Adam

• 使用最广泛的方法
• 记录一段时间的梯度平方和（累死Adadelta和RMSprop），以及梯度的和（类似Momentum动量）
• 把优化看做铁球滚下山坡，Adam定义了一个带动量和摩擦的铁球

实现方法

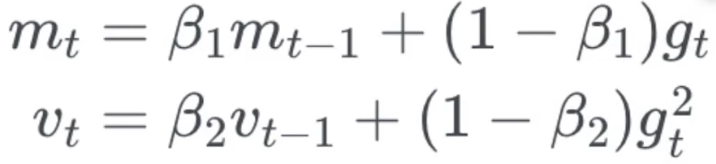
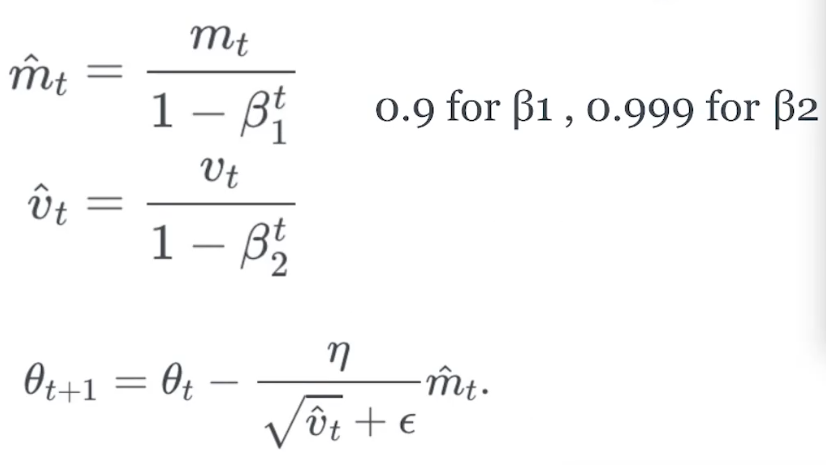
更新权值采用原来的权值减去某一梯度的变形

如何选择

• 如果数据集是稀疏的，选择自适应学习率的方法会更快的收敛
• RMSprop,Adadelta,Adam的效果非常相似，大多数情况下Adam略好

小技巧

• 每一个epoch之前重新洗牌数据

• 使用Batch Normalization

  • 我们一般会对训练数据做正则化，但是随着数据的前馈，后面layers的输入已经不是正则化的了，Batch Normalization就是在后面layer之间做正则化
  • 使得训练可使用更大的学习率，layer参数的初始化可以更加随意
  • BN还有regularization的作用，可以减少对Dropout的依赖

• Early Stopping:Early stopping (is) beautiful free lunch (NIPS 2015 Tutorial slides ,slide 63)

• 增加随机噪声到梯度

  • 使得layer参数初始化更加随意
  • 使得model可以找到新的局部最小值

许可协议

本文采用 署名-非商业性使用-相同方式共享 4.0 国际 许可协议，转载请注明出处。

分享文章