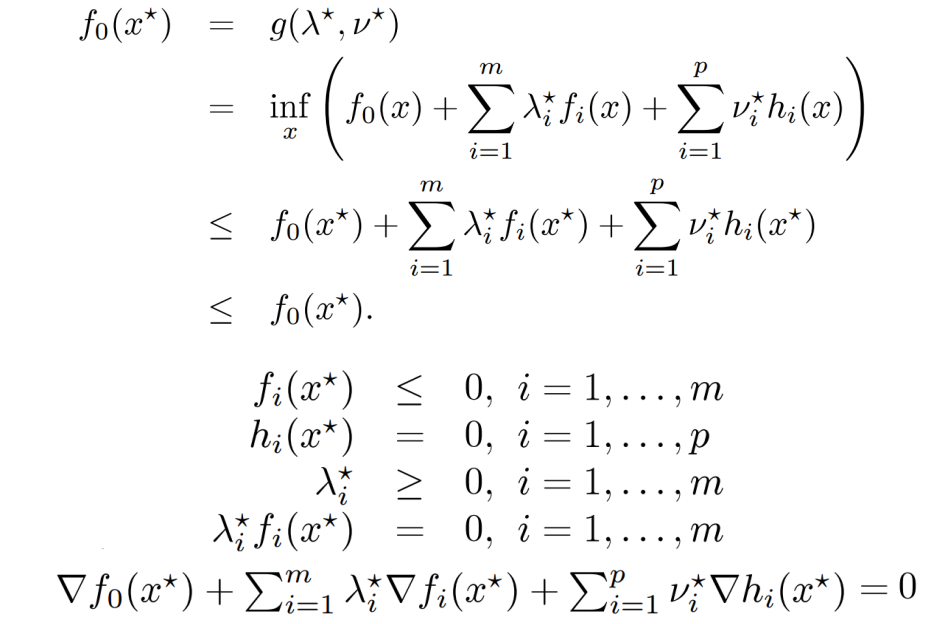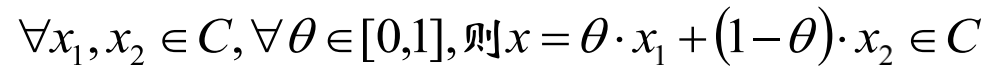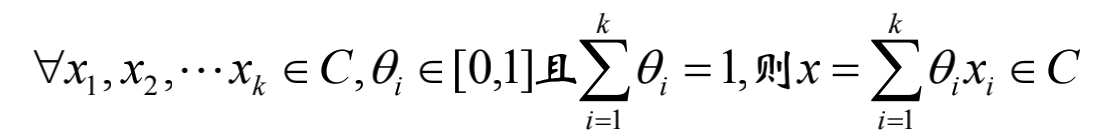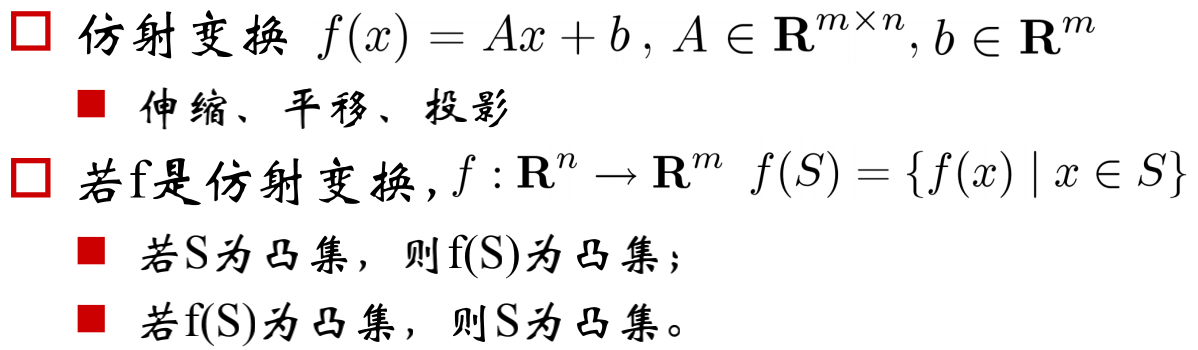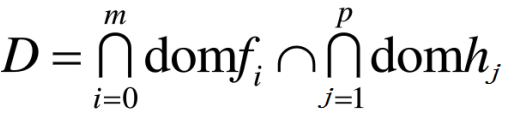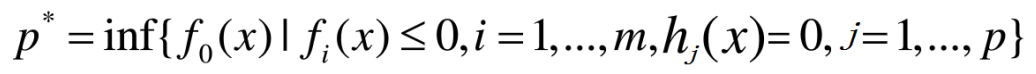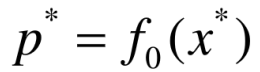主要内容
- 凸集的基本概念
- 凸函数的基本概念
- 凸优化的一般提法
凸集基本概念
思考两个不能式
两个正数的算术平均数大于等于几何平均数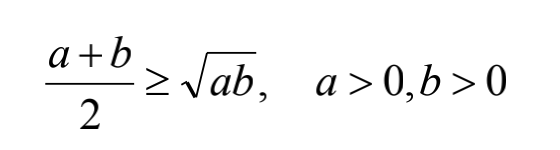
给定可逆对称阵Q,对于任意向量x,y,有: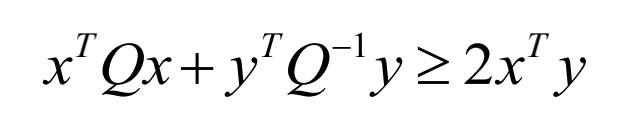
思考凸集和凸函数
在机器学习中,我们把形如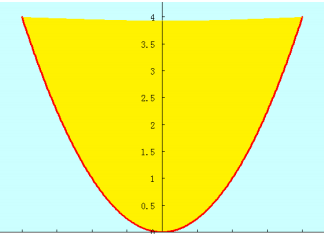

这样的图形的都称为凸函数。
*是凸函数,函数图像上位于的区域构成凸集。
- 凸函数图像的上方区域,一定是凸集;
- 一个函数图像的上方区域为凸集,则该函数是凸函数。
直线的向量表达
已知二维平面上的两定点A(5,1),B(2,3)尝试给出经过带你AB的直线方程: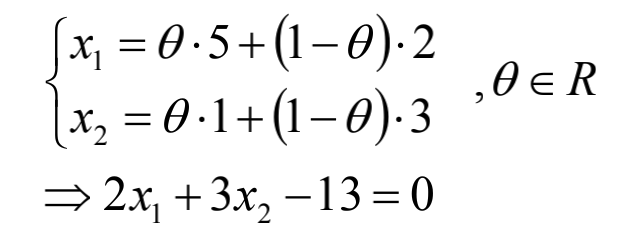
写成向量形式: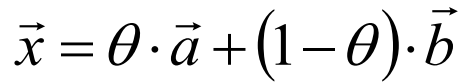
其中: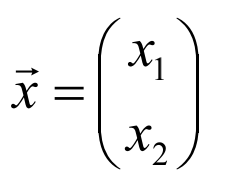
几何体的向量表达
已知二维平面上的两个定点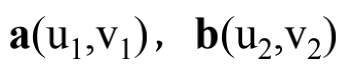 ,则:
,则: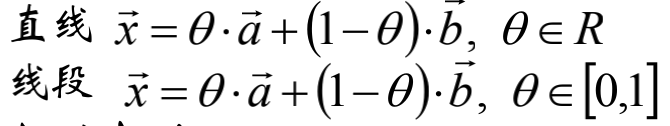
推广到高维: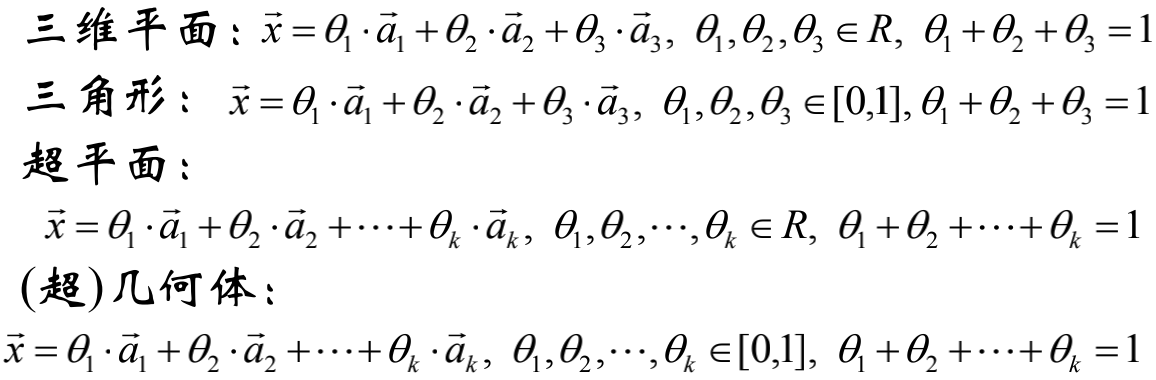
仿射集(Affine set)
定义:通过集合C中任意两个不同点的直线仍然在集合C内,则称集合C为仿射集。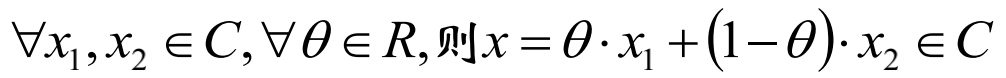
仿射集的例子:直线、平面、超平面
超平面:
f(x)=0表示定义域在的超曲面:令,则表示截距为b的超平面。
n维空间的n-1维仿射集为n-1维超平面
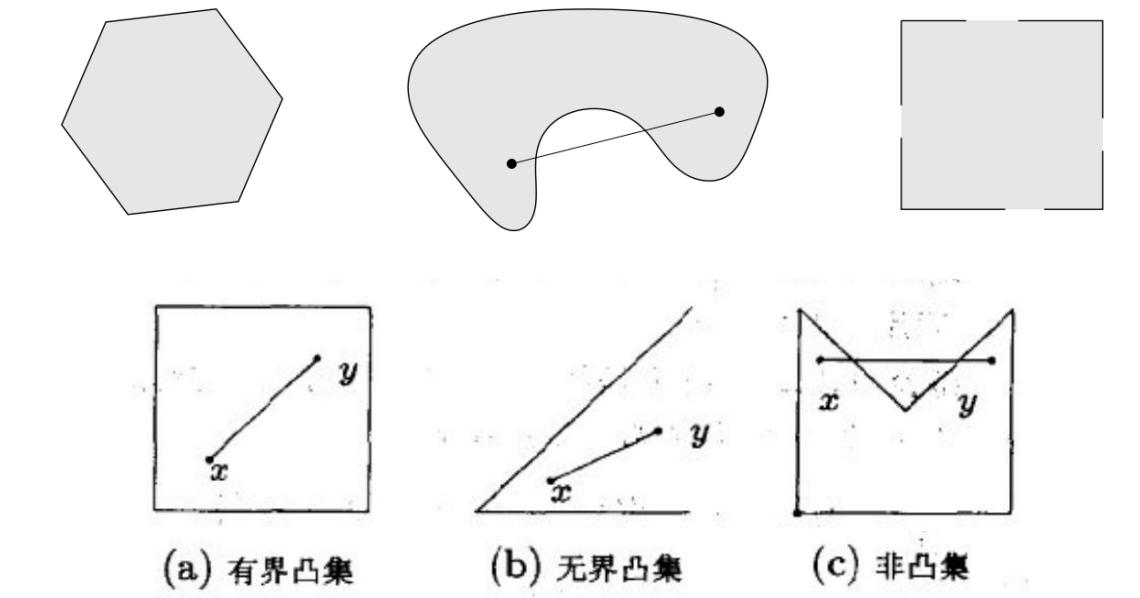
凸集
集合C内任意两点间的线段均在集合C内,则称集合C维凸集。
注意和仿射集区分
仿射集是凸集的一种特殊形式,仿射集一定是凸集。
k个点的版本:
凸包
集合C的所有点的凸组合所形成的集合,叫做集合C的凸包: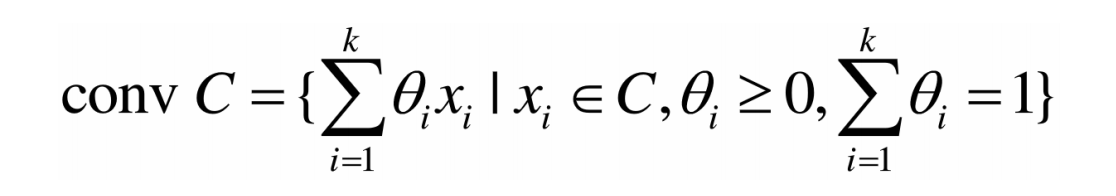
集合C的凸包是能够包含C的最小凸集。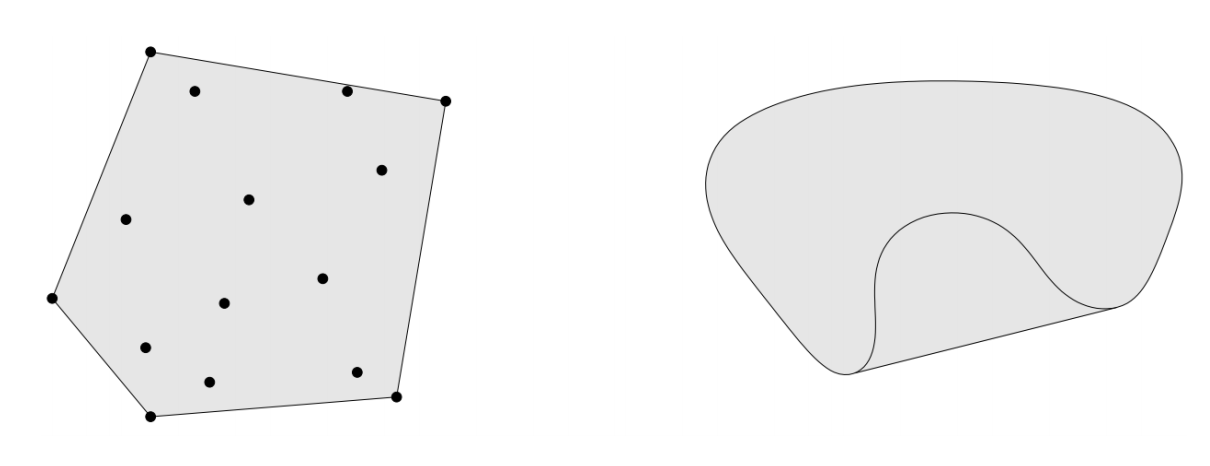
超平面和半空间
超平面:hyperplane
半空间:halfspace
{xa^Tx\le b}$$$${xa^Tx\ge b}
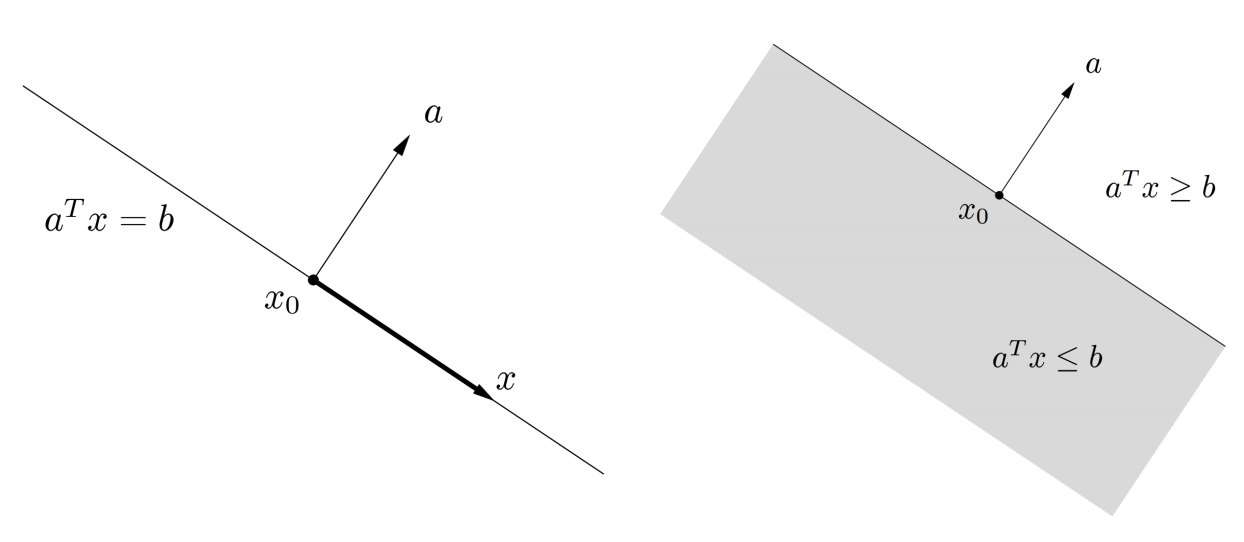
欧式球和椭球
欧式球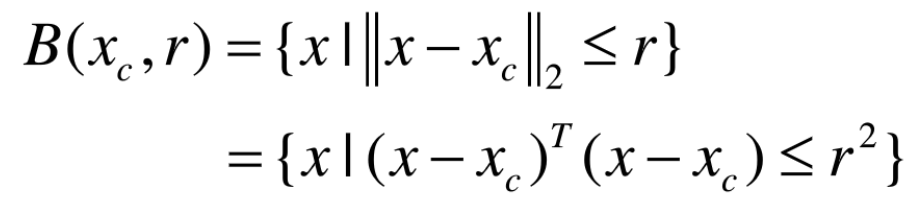
椭球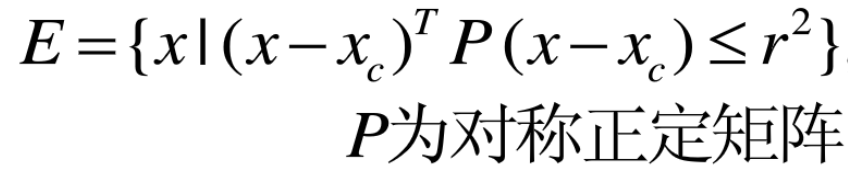
范数球和范数锥(欧式空间推广)
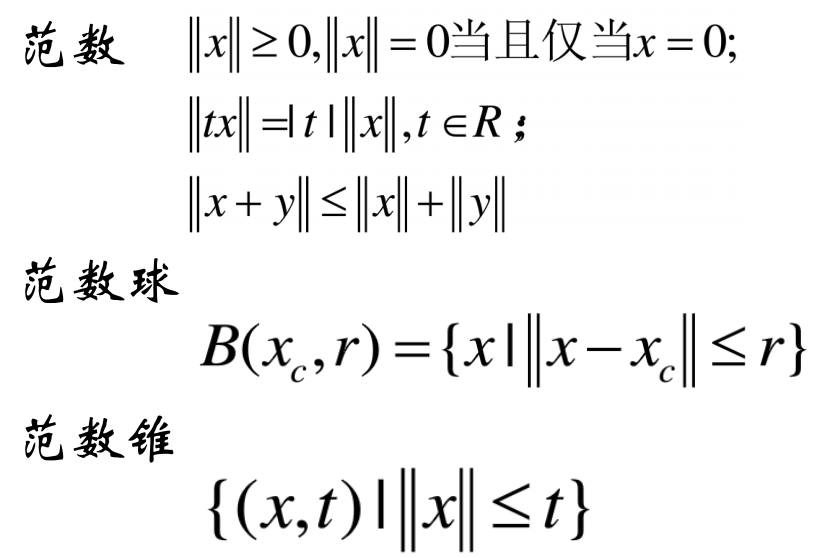
###空间中的二阶锥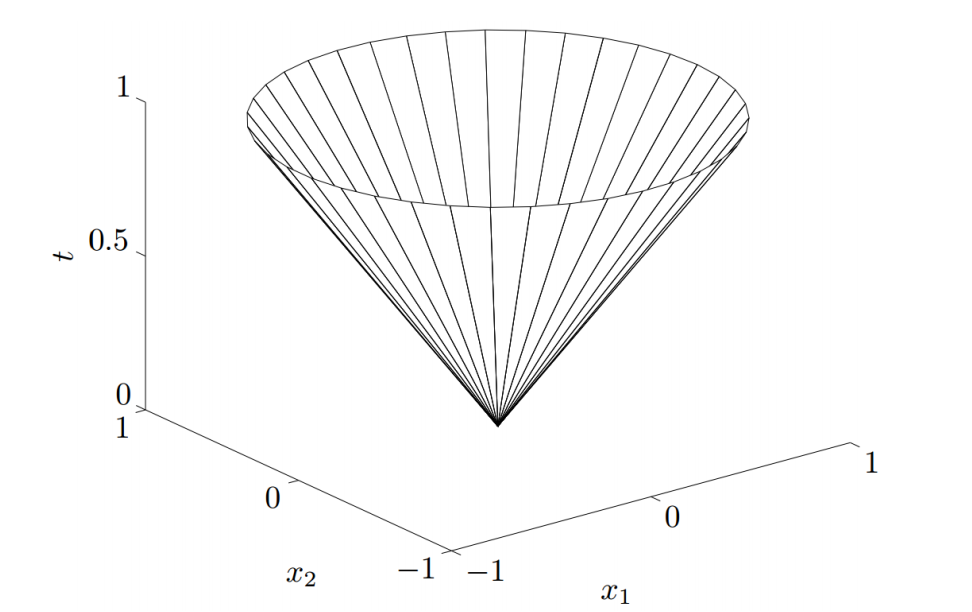
多面体
有限个半空间和超平面的交集。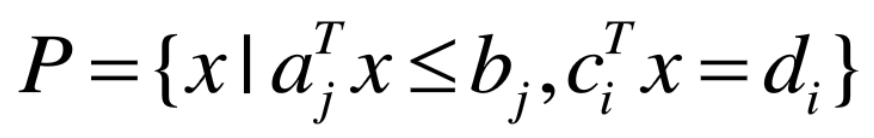
仿射集(如超平面、直线)、射线、线段、半空间都是多面体
多面体是凸集
此外,有界的多面体有时称作多胞体(Polytope)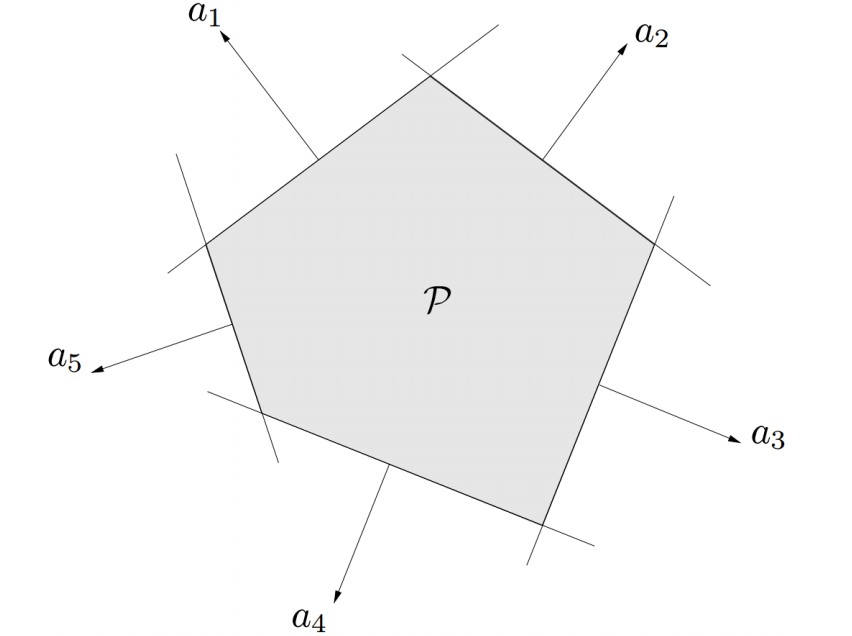
保持凸性运算
- 集合交运算
- 仿射变换
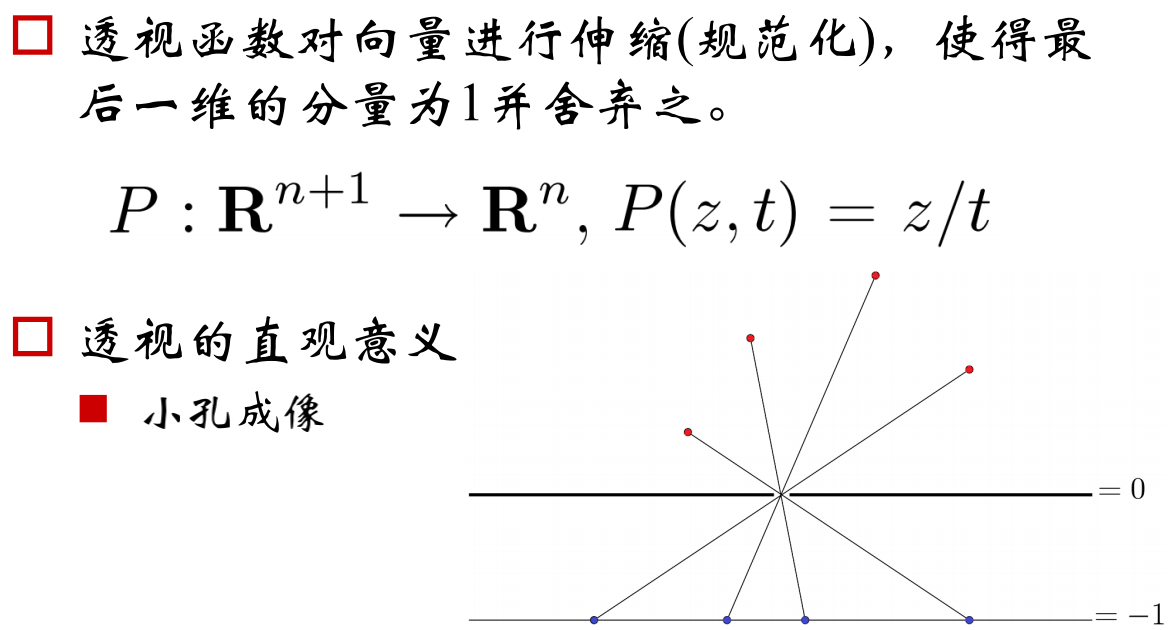
- 透视变换
- 投射变换(线性分式变换)
集合交运算:半空间的交
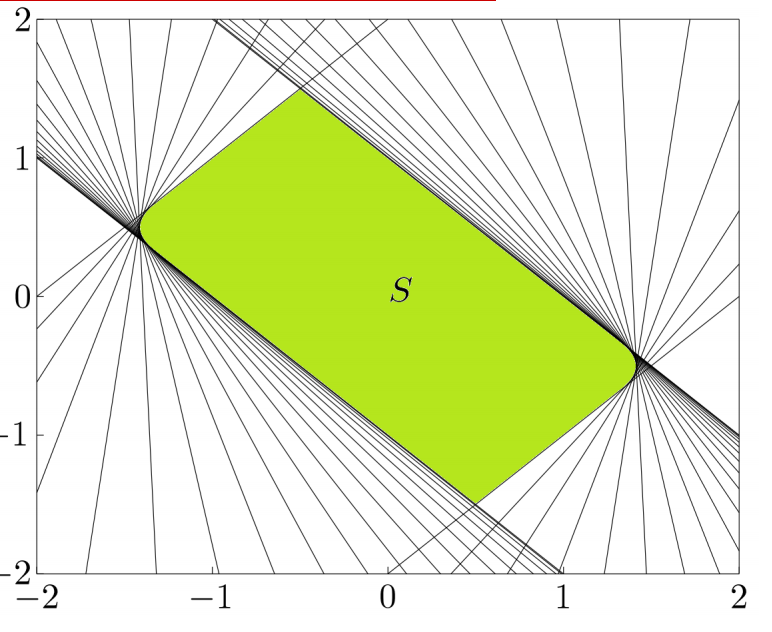
仿射变换
透视变换
投射函数(线性分式函数)
分割超平面
设C和D为两不相交的凸集,则存在超平面P,P可以将C和D分离。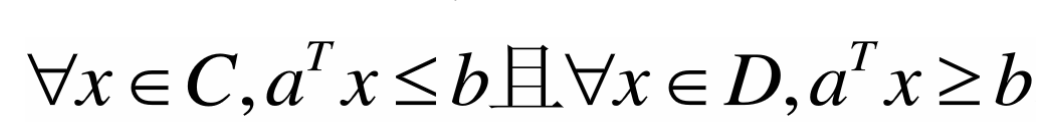
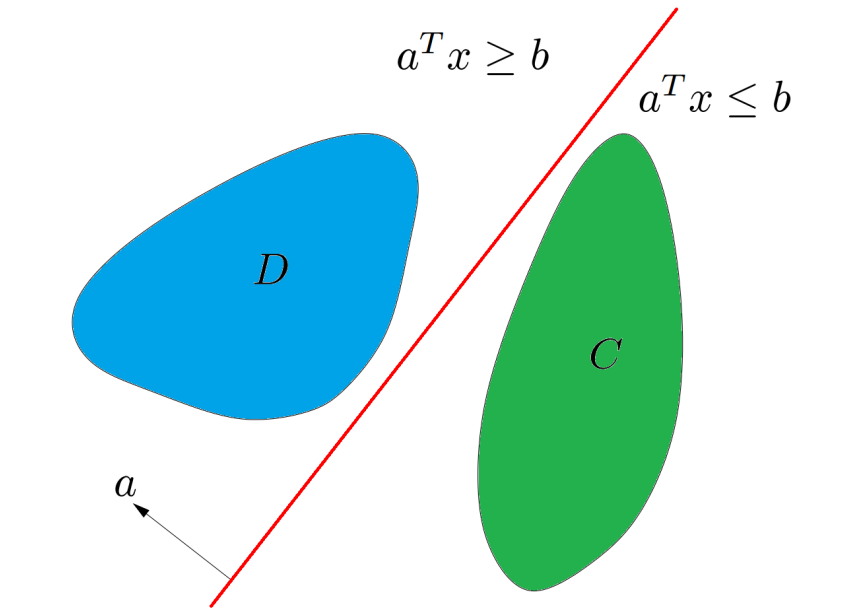
分割超平面的构造: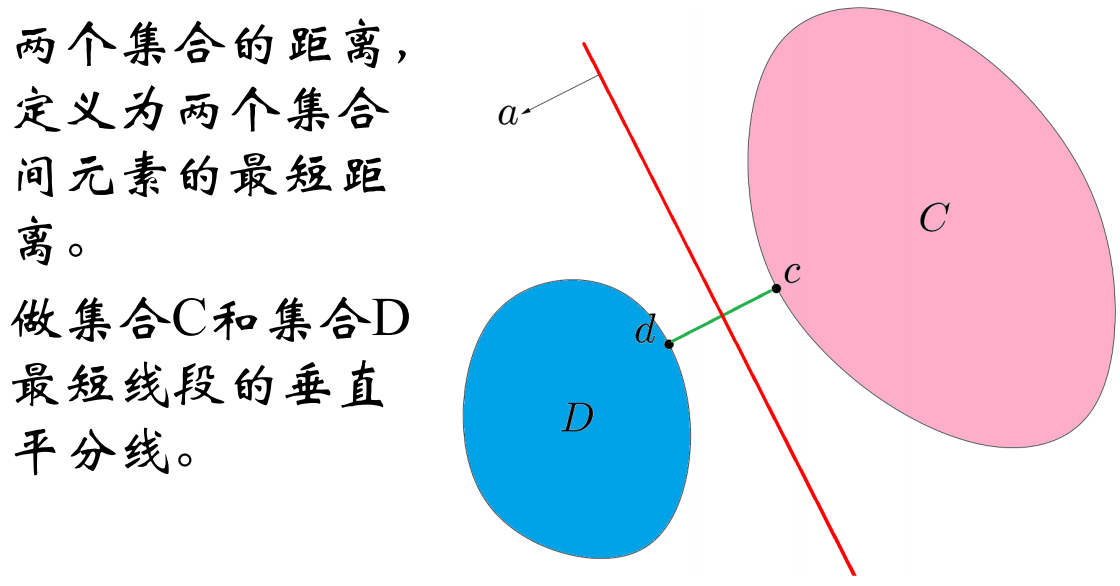
支撑超平面
设集合C,x0是C边界上的点,若存在。满足对任意,都有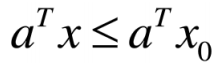 成立,则称超平面
成立,则称超平面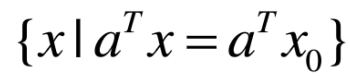 为集合C在点x0处的支撑超平面。
为集合C在点x0处的支撑超平面。
凸集边界上任意一点,均存在支撑超平面。
反之,若一个闭的非中空集合,在边界上任意一点存在支撑超平面,则该集合为凸集。
凸函数
若函数f的定义域domf为凸集,且满足: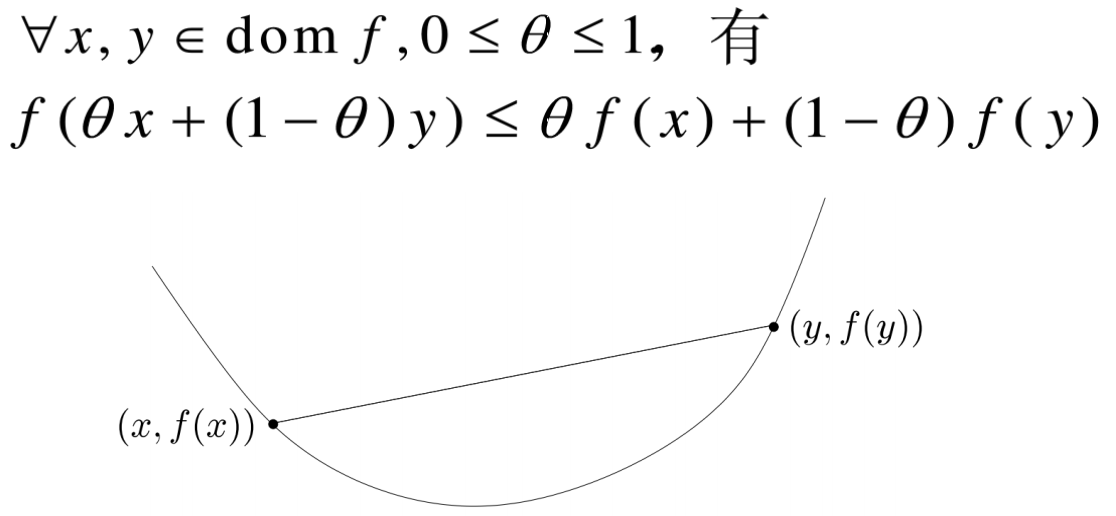
一阶可微
若f一阶可微,则函数f为凸函数,当且仅当f的定义域domf为凸集,且: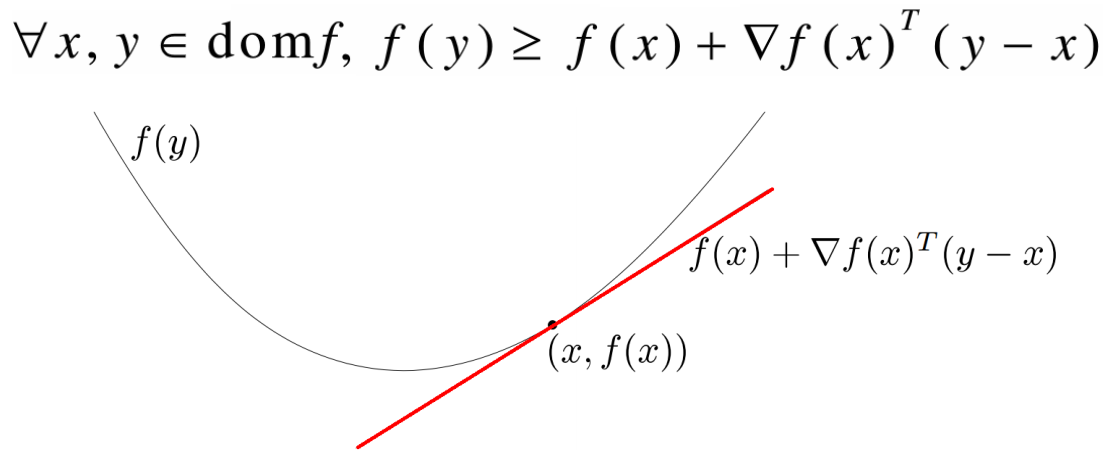
分析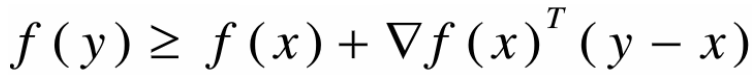
对于凸函数,其一阶Taylor近似本质上是该函数的全局下估计。
反之如果一个函数的一阶Taylor近似总是其全局下估计,则该函数是凸函数
该不等式说明从一个函数的局部信息,可以得到一定车程度的全局信息。
二阶可微
若函数f二阶可微,则函数f为凸函数当且进档dom为凸集,且: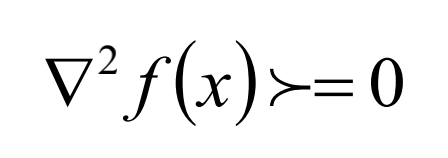
若f为一元函数,上式表示二阶导大于等于0
若f是多元函数,上式表示二阶导Hessian矩阵半正定。
凸函数举例:
上镜图
函数f的图像定义为: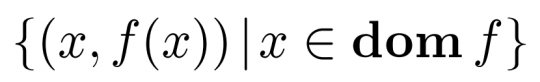
函数f的上镜图(epigraph)定义为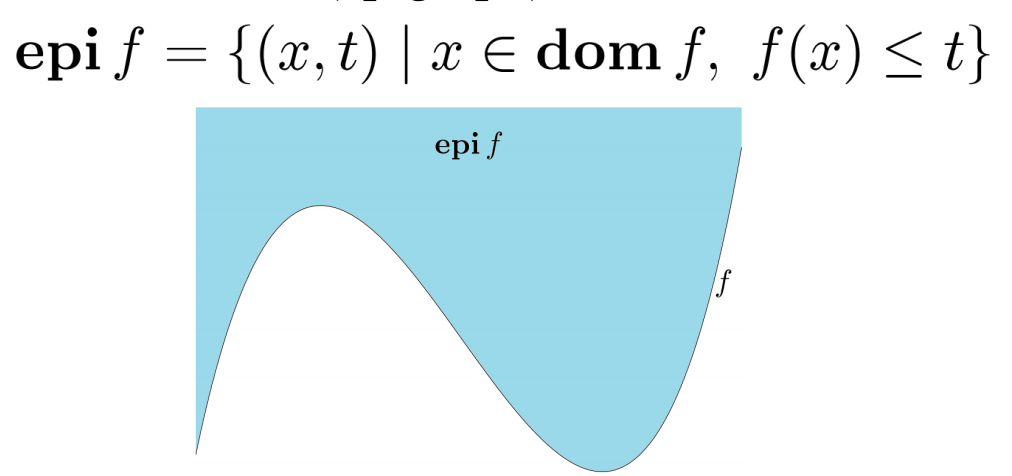
Jensen不等式:若f是凸函数
基本Jensen不等式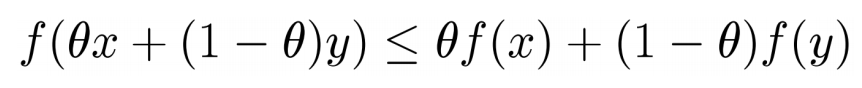
若: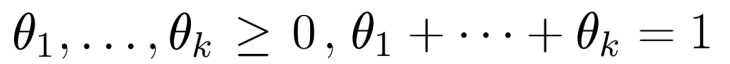
则: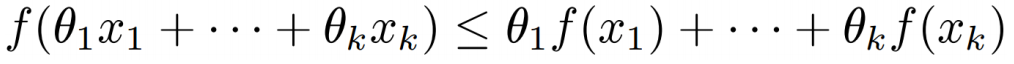
若: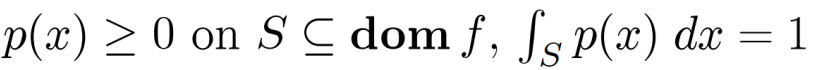
则: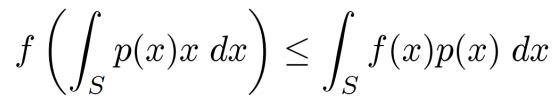
Jensen不等式是几乎所有不等式的基础
保持函数凸性的算子

凸函数的逐点最大值
若均为凸函数,定义函数: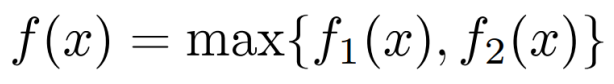
则函数为凸函数。
证明: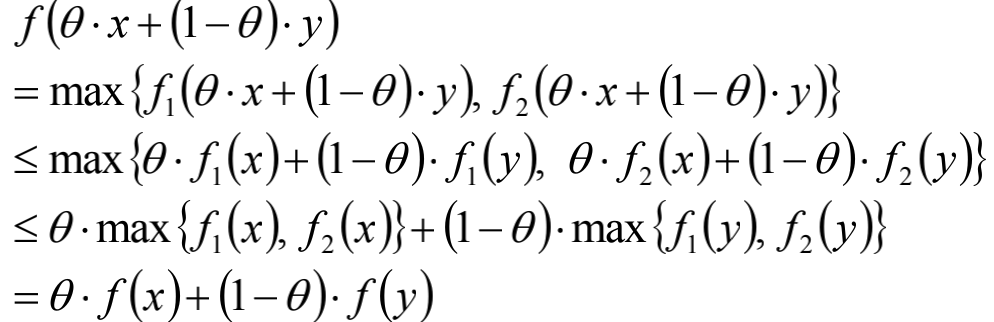
第二个不等号的表达: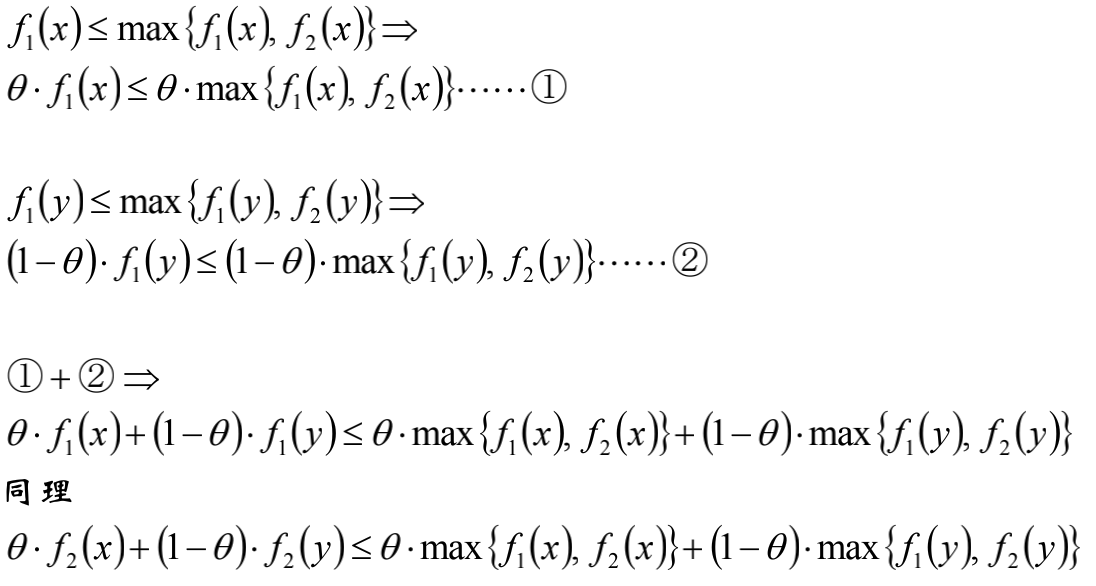
第二个不等好的形式化表达:
共轭函数
原函数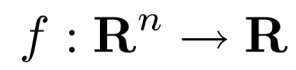 ,共轭函数定义:
,共轭函数定义: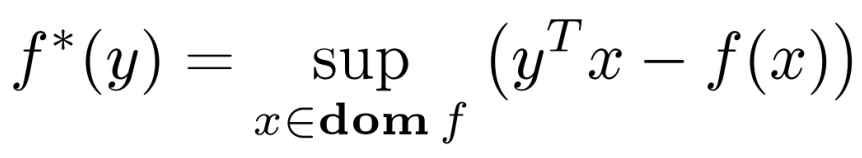
显然,定义式的右端是关于y的仿射函数,他们逐点求上确界,得到的函数f*(y)一定是凸函数。
理解: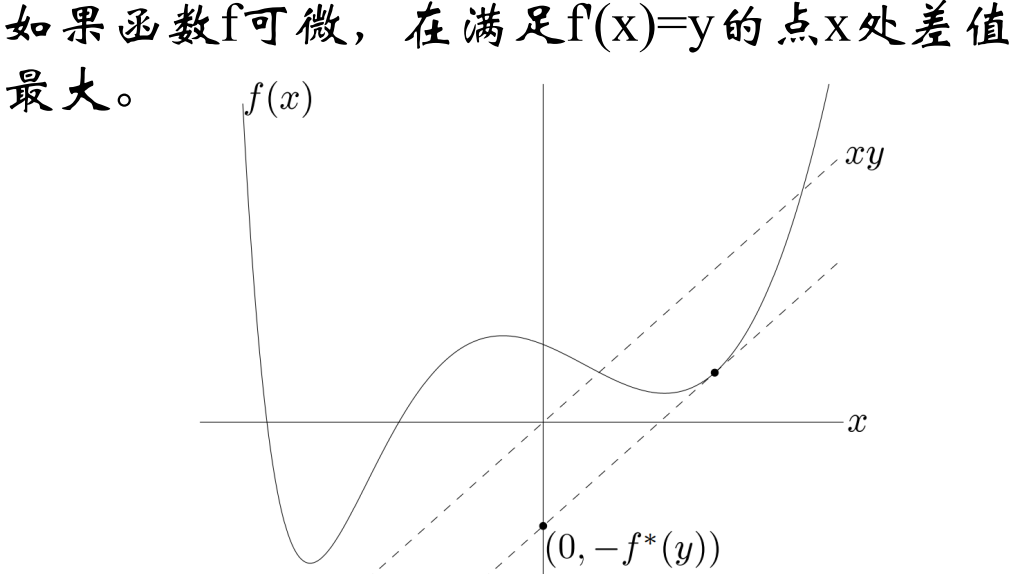
例:
求共轭函数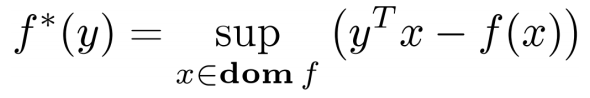
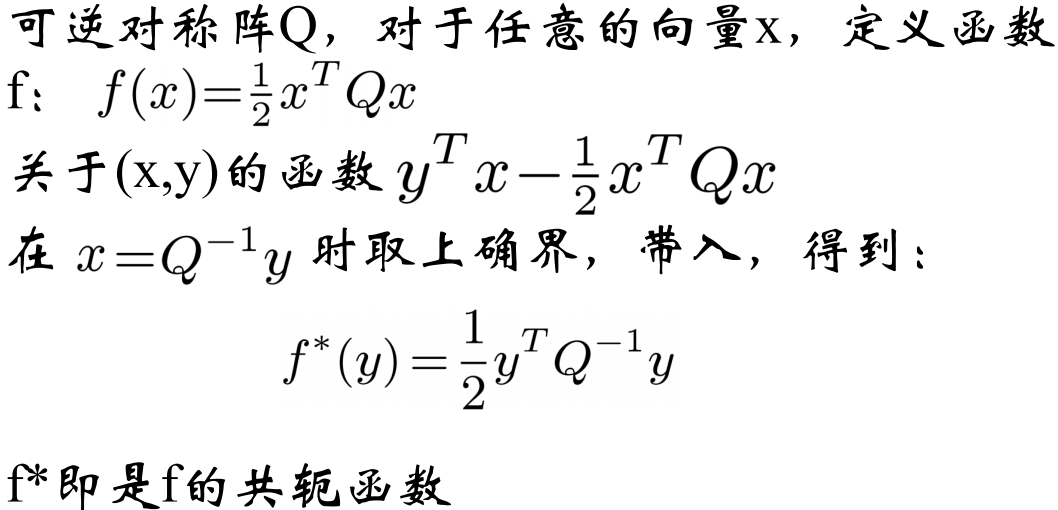
Fenchel不等式
根据共轭函数定义: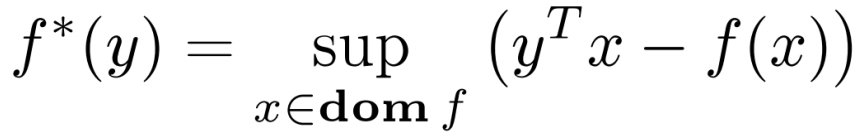
易得: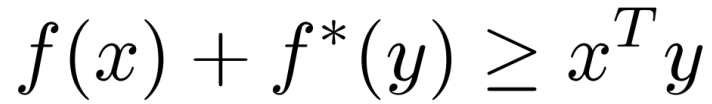
应用: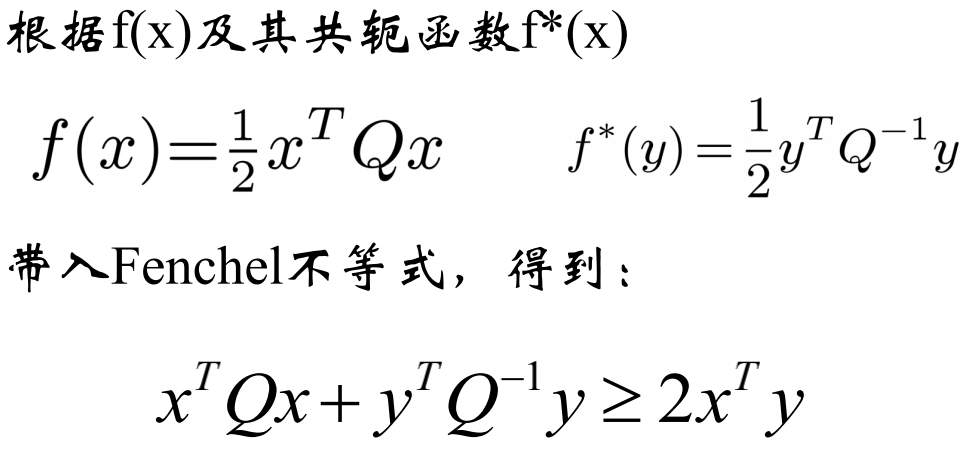
凸优化
凸优化问题的基本形式:
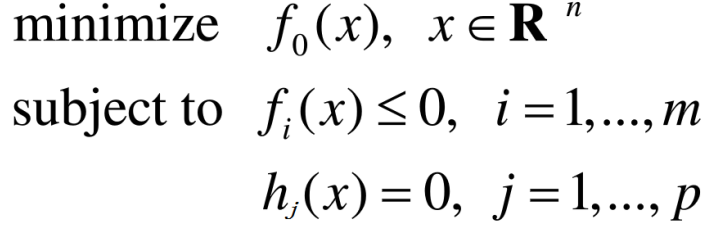
- 优化变量:
- 不等式约束:
- 等式约束:
- 无约束优化:
- 优化问题的域:

- 可行点(解)(feasible)

- 可行域(可解集)
所有可行点的集合。 - 最优化值

- 最优化解

对于
其中
为凸函数,为仿射函数
凸优化问题的重要性质: - 凸优化问题的可行域为凸集
- 凸优化问题的局部最优解就是全局最优解
对偶问题
一般优化问题的Lagrange乘子法
Lagrange函数: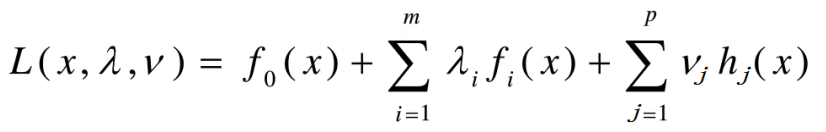
对于固定的x,Lagrange函数是关于和v的仿射函数。
Lagrange对偶函数
Langrange对偶函数: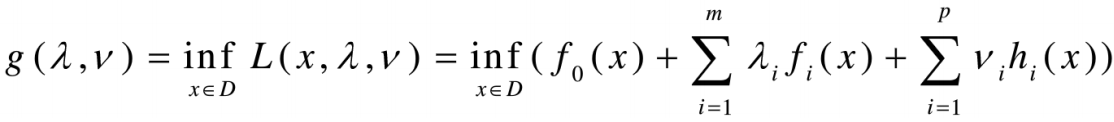
若没有下确界,定义: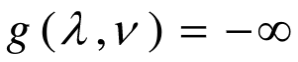
根据定义,显然有:对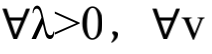 ,若原优化问题有最优值P*,则:
,若原优化问题有最优值P*,则: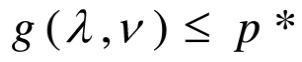
进一步:Lagrange函数对偶函数为凹函数。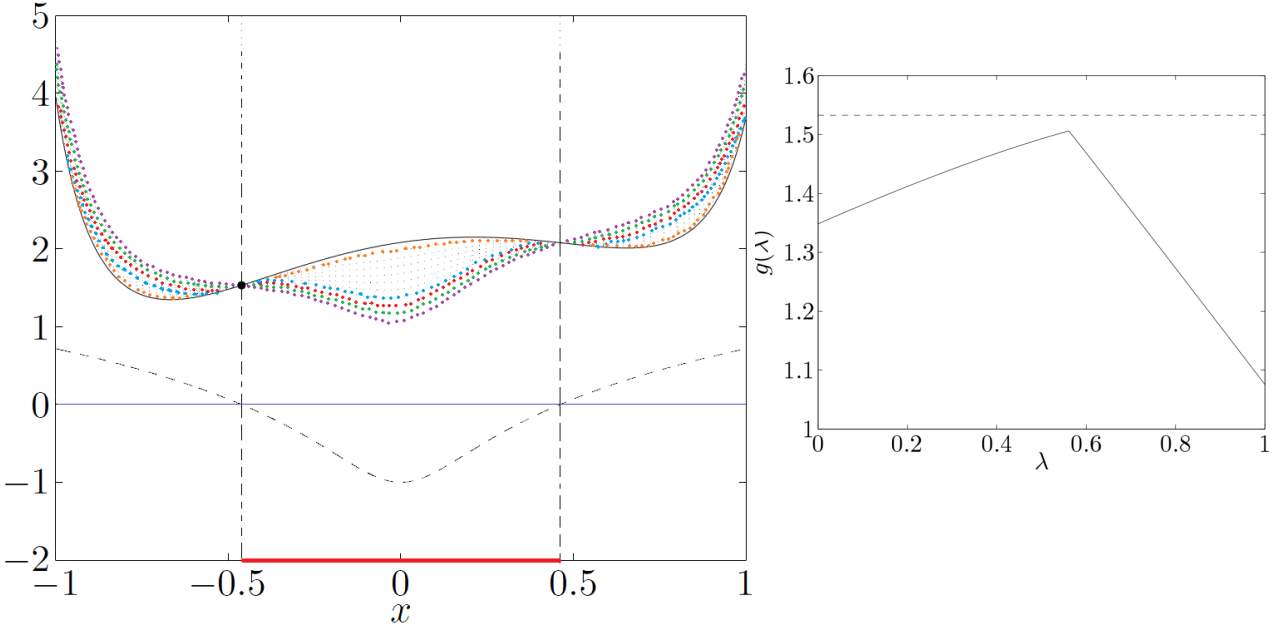
鞍点解释

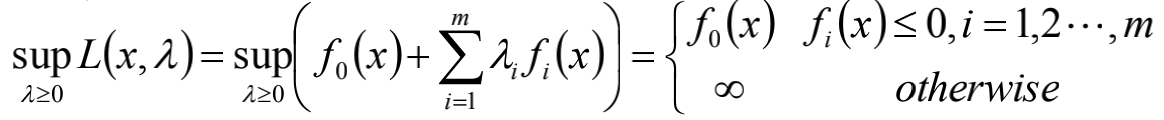
鞍点:最优点
强对偶条件
若要对偶函数的最大值即为原问题的最小值,需要满足的条件: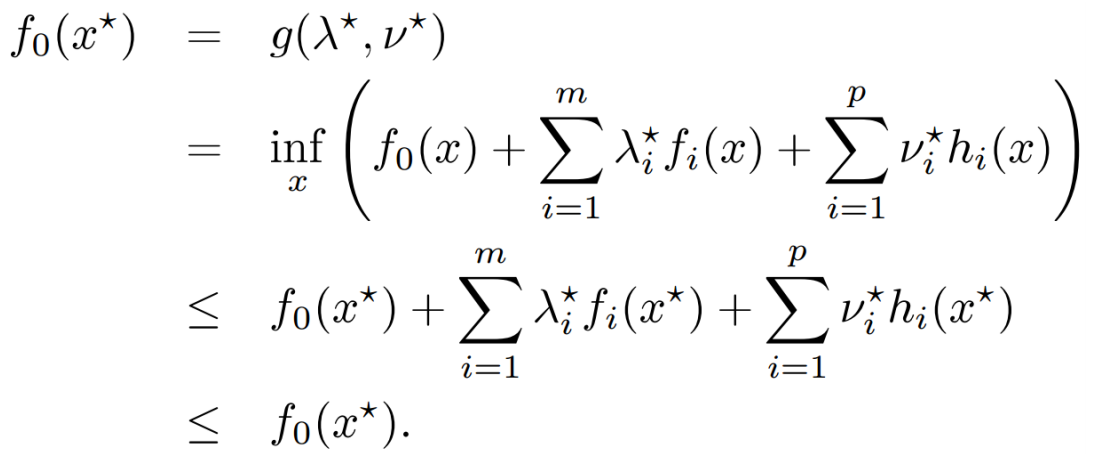
Karush-Kuhn-Tucker(KKT)条件